Los chicos del calentamiento global dejan a una baronesa del gobierno (UK) con el culo al aire.

Se trata de la baronesa Verma, Ministra de Energía y Cambio Climático del Reino Unido. Le ha salido un grano en el culo, en forma de tándem entre un lord, de la casa de tales, y un matemático. El lord es Lord Donoughue, y el matemático es Doug Keenan.

Es una historia aburridísima, y además absurda. Pero sutil. Algo cercano a diez preguntas parlamentarias, siempre la misma con distinta formulación, tratando de obligar al Met Office a confesar que el calentamiento global no es “estadísiticamente significativo” - aunque siempre afirme lo contrario. El Gobierno de Su Majestad usa lo que le pasa la oficina meteorológica, y difunde alegremente el cuento del calentamiento global. Y Doug Keenan debió explicarle a Lord Donoughue que esos registros de temperatura que enseñan como demostración del calentamiento y gran alarma, no son estadísticamente significativos. Esto es, que no son diferenciables del azar si se analizan adecuadamente. Que no hay nada necesariamente “raro” (o antropogénico) en ellos.

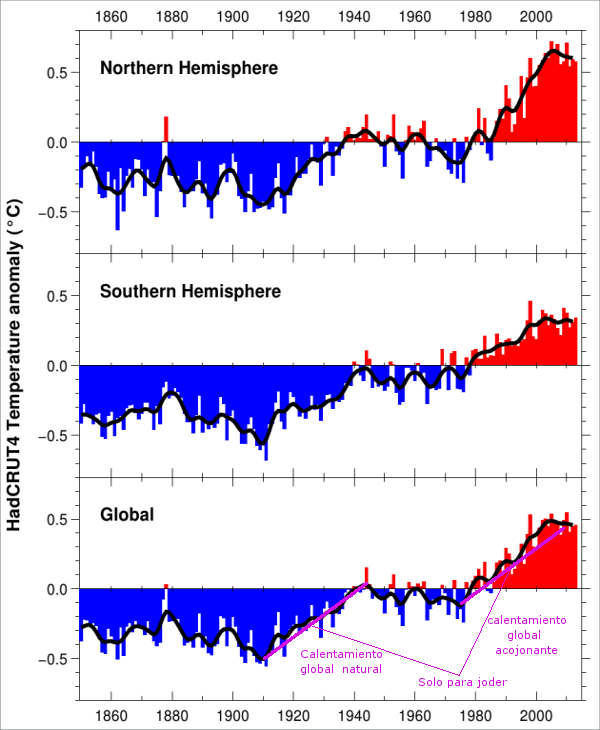La idea es sencilla, si no se entra en los detalles. Para decir que algo es "estadísticamente significativo", y fuera del simple azar, necesitas un modelo estadístico. Por ejemplo, si te salen diez caras seguidas al tirar una moneda, dices que el resultado es estadísticamente significativo porque es muy improbable que se deba al azar. Es más fácil pensar que la moneda está trucada. Y el modelo estadístico que estás usando para juzgarlo es uno que dice que hay la misma probabilidad, un cada tirada, de que salga cara o que salga cruz.

Para diferentes series de datos suele haber más de un modelo estadístico posible. Pero se puede calcular qué modelo es mas probable. Por ejemplo, el modelo A es 10 veces más probable que el modelo B. Y Doug Keenan le mostró a Lord Donoughue que el modelo estadístico que usa el Met Office (ahora se puede decir usaba), es manifiestamente inválido, y mil veces menos probable que otro modelo estadístico muy usual. El ARIMA (3,1,0) para los que se enteren, pero a los demás nos da lo mismo. Lógicamente, hay que dar una razón muy poderosa para usar un modelo mucho menos probable estadísticamente. Y de ahí ha venido el rosario de preguntas parlamentarias / grano en el culo. Hasta que el Met Office ha tenido que confesar que no usa un modelo estadístico (después de haber dicho que sí), sino modelos climáticos. En cuyo caso supongo que el calentamiento no es "estadísticamente significativo", sino imaginariamente significativo - según esos modelos que sabemos que no funcionan. Una doble mentira al parlamento.

Lo lleva contando Bishop Hill desde el principio, y este es el último grito.

• Poor old Baroness Verma

Lord Donoughue (Labour): To ask Her Majesty’s Government, further to the Written Answer by Baroness Verma on 8 November 2012 (WA 224–5) stating that “the temperature rise since about 1880 is statistically significant” and the Written Answer by Baroness Verma on 21 January (WA 99) stating that the Government do not use “purely statistical models” to analyse global temperatures, whether they will reconsider the earlier assertion that the rise in global temperatures since 1880 is “statistically significant”.

Baroness Verma (Conservative):  With regards to the Written Answer I gave the Noble Lord on 8 November 2012 (Official Report, Column WA 224-5), I have nothing further to add beyond my previous answers on this subject.

Y son mentiras del gobierno. Las preguntas se hacen al gobierno, y este delega en el ministro. Baronesa Verma. Que  su vez le pide la respuesta al Met Office. Cuyo director no tiene ni idea de estadística, y delega en su Jefe Científico. Julia Slingo.

Para eso se han tirado meses y meses de preguntas y preguntas. A veces contestando chorradas, y a veces no contestando (4 veces). Hasta que se ha formado un pequeño escándalo interno en la cámara. Con muchos miembros de la cámara, y funcionarios, mosqueados. Y al final han tenido que contestar -si no confesar todavía- lo que no querían contestar. Espero que sigan las preguntas, hasta que tengan que decir que es cierto, que donde decían "estadísticamente significativo" no era cierto. Y que donde decían que usaban tal modelo estadístico (no válido), solo era una mentira.

Lo gracioso es que Doug Keenan también se ha carteado con miembros del Met Office. Para preguntar por qué no contestaban. Con el director, con Slingo, y con uno que sí sabe de estadística. Y este último le decía que sí, que el modelo que alegaba el Met Office (antes de decir que no usa modelos estadísticos), no vale.

Con intercambios tan hilarantes con el director del MO como este:

Last week, Lord Donoughue tabled Parliamentary Question HL6132, about statistical models of global temperature data. HL6132 is essentially the same as HL5359, which the Met Office refused to answer. The Met Office Chief Scientist does not have the statistical skills required to answer the Question; there is, however, at least one scientist at the Met Office who does have the skills—Doug McNeall. I ask you to ensure that the Question is answered. [-->]

Bien, pues ahora sabemos, gracias al parlamentarismo británico, que el calentamiento global no es "estadísticamente significativo". Y que si no es por unos modelos que no funcionan, no hay manera de decir que no sea natural. Ni mucho menos en qué medida. Por cierto, Lord Donoughue es laborista. Muy partidarios de la alarma del clima. Pero le toca las narices que el gobierno mienta - aunque sea a favor de una causa del partido. Como aquí, más o menos.

La historia de la tortura de la baronesa Verma es larga, como se puede imaginar. Siempre en lo de Bish:

• Not answering the question (17/04/2013)
• Advisers advise politicians to look in the peer-reviewed literature (23/04/2013)
• Another MP develops an interest in statistics (24/04/2013)
• No let-up for the Met Office (9/05/2013)
• Met Office admits claims of significant temperature rise untenable (27/05/2013)
• Met Office responds to Keenan (31/06/2013)
• More slipperiness from Baroness Verma (22/07/2013)
• More cesspit (17/01/2014)
• Poor old Baroness Verma (6/02/2014)