El calentamiento global "escondido" en el fondo del mar, ni es "calentamiento", ni es problema.
Aunque creo que ya lo hemos comentado, esto es algo en lo que hay que hacer hincapié. Y aprovechamos una entrada y un dibujo de WUWT.
A cuenta de La Pausa en el "calentamiento global", el primer argumento alarmista -y el más extendido- es que no hay Pausa, sino que el calor se está yendo a otro sitio diferente. En concreto, al fondo del mar [-->]. ¿Y por qué al fondo? Pues porque en la superficie lo medimos bastante bien, y no ahí no se ve un calentamiento como el que le falta a la teoría de los calentólogos. Lo divertido es que ese calor que se habría escondido en el fondo del mar no podría ser un problema ni siquiera para la imaginación más calenturienta.El dibujo de Werner Brozek que explica muy gráficamente en WUWT es este, y representa una bola de acero de 4 kilogramos junto a un perdigón de 4 gramos, del mismo acero.
Imagina que las dos esferas están a la misma temperatura, y que calientas una de ellas en 1ºC y después las pones en contacto. Es muy distinto lo que pasa, según cuál elijas para calentar antes de juntarlas.

Si calientas el perdigón, tendrá 1º mas de temperatura que la bola, y al untarlos le va a pasar calor a la bola. Hasta que se pongan a la misma temperatura. ¿Qué temperatura va a ser esa, cuando se igualen las temperaturas de las dos esferas? Como la capacidad calorífica de la bola es mil veces mayor que la del perdigón (pesa mil veces más), la temperatura va a ser la misma que tenían antes de empezar. El perdigón pasará todo su calentamiento a la bola, y el conjunto de las dos no aumentará de temperatura. Bueno, aumentará 0,001ºC, que es lo mismo que nada. No se puede notar.
Si en vez de calentar el perdigón 1ºC, lo calientas 10ºC, y después juntas las dos esferas, lo que conseguirás al final es que ambas se queden a una temperatura 0,01ºC superior a la que empezaron. Otra vez nada.
Si haces lo contrario, si subes de temperatura la bola de 4 kilogramos en 1º, y después las juntas, lo que ocurrirá al final es que ambas acaban con un grado más de temperatura. La diferencia está en que has necesitado mil veces mas calor para aumentar en 1ºC la temperatura de la bola que la del perdigón.
Toda la chorrada de que ese calor que imaginan “escondido en el mar” es que, para que fuera un problema, el calor tendría que tener un sistema para volver al aire. Y no lo tiene. Una vez igualadas las temperaturas (en +0,001ºC), el calor no se mueve. O tendría que calentar el mar para que al menos fuera un problema para el mar. Pero como el mar tiene mil veces más capacidad calorífica que la atmósfera, la situación es la misma que la de la bola y el perdigón de los que hablamos.
Es verdad que el calor que no está calentando la atmósfera durante La Pausa del “calentamiento global” podría estar calentando el mar. Pero de tal forma que si el calor que no se ve en el aire, fuera una cantidad de calor que lo hubiera calentado 3,2ºC en un siglo (esa es la teoría) en caso de no haber habido La Pausa; ese mismo calor, llevado al mar, supondría un aumento de temperatura del mar de 0,003ºC. Y no lo podrías ni siquiera medir – no hablemos ya de notar.
En resumen. Si dicen que La Pausa no es cierta porque el calor se ha “escondido en el fondo del mar”, están diciendo una chorrada. Porque ese calor se ha perdido para siempre – a todos los efectos que nos pueden interesar.
Nota técnica. En realidad el mar se está calentando mucho más que esos 0,003ºC / siglo. En lo que se puede medir (bastante mal), parece que como unos 0,2ºC / siglo en la mitad superior del mar, y -aparentemente- nada en la mitad inferior. La media sería 0,1ºC / siglo.
El gráfico de la mitad superior:
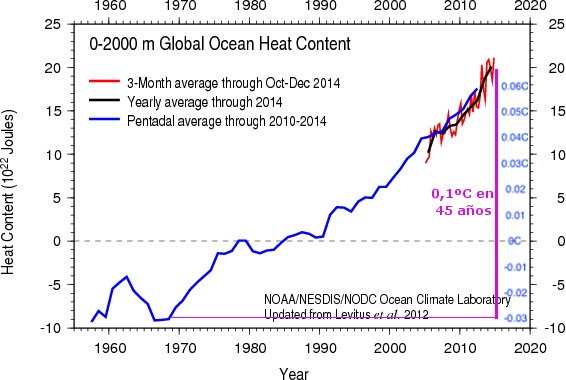
Lo que pasa es que la teoría de los calentólogos ya cuenta con calor que va al mar. Y la diferencia, a cuenta de La Pausa, es que en vez de ir al mar (sólo) la mayor parte del calentamiento, se estaría yendo el 100%. Pero ese calor de diferencia entre “la mayor parte se va al mar” y “el 100% se va al mar”, que en temperatura del aire representa 3,2ºC, en temperatura del mar supone mil veces menos. O 0,003ºC. O, literalmente, nada.




 Dices:
- mientras que la capa superior de 0 a 700 mts , se _a ralentizado su calentamiento incluso enfriado..
Una imagen vale más que mil palabras. No se ven cambios dignos de mención desde 1983 de 0 a 700m.
Dices:
- mientras que la capa superior de 0 a 700 mts , se _a ralentizado su calentamiento incluso enfriado..
Una imagen vale más que mil palabras. No se ven cambios dignos de mención desde 1983 de 0 a 700m.
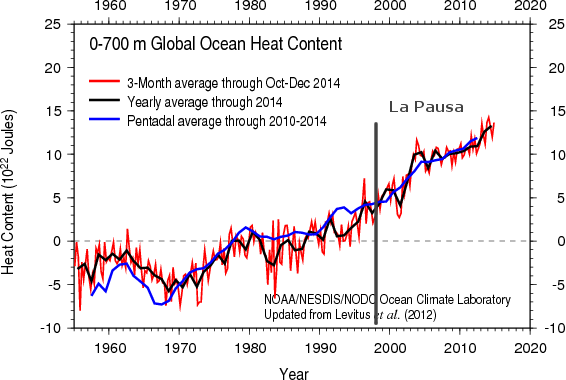 - Lo que pasa mas halla de los 2000mts es despreciable para las escalas de tiempo que nos interesa ,esto ( ya te lo dije mas arriba )
Y lo que pasa debajo de los 700 también. Si queires que sea El Niño / La Niña lo que produce La Pausa, entonces el Calentamiento Global (1975 - 1998) tuvo contriibución de El Niño / La Niña. Y si durante La Pausa ese ciclo se lleva casi todo el "calentamiento antropogénico", entonces la fuerza de ese calentamiento es igual a la del ciclo. Y el Calentamiento Global Acojonante no era todo antropogénico, sino sólo la mitad.
Trenberth, primer enlace:
- “The picture emerging is one where the positive phase of the PDO from 1976 to 1998 enhanced the surface warming somewhat by reducing the amount of heat sequestered by the deep ocean, while the negative phase of the PDO is one where more heat gets deposited at greater depths, contributing to the overall warming of the oceans but cooling the surface somewhat.
No puedes jugar a todo. Bueno, es lo que hacen los alarmistas, pero es trampa. Si el "calor perdido" va al fondo del mar, entonces es como si hubiera desaparecido, para lo que nos importa. Y si el calor de La Pausa que no hay está en el juego El Niño / La Niña (que lo suelen medir hasta los 350 metros), entonces el efecto del CO2 es como la mitad de lo que dicen los modelos que no contaban con La Pausa.
- Ahora esto es un ciclo y el proceso se invertirá inevitablemente , la capa superior se volverá menos eficiente en transportar energía hacia las capas profundas ,como consecuencia esta se calentara mucho mas y la energía que antes iba a parar a las capas profundas se quedara en superficie calentando la atmósfera en el proceso..
Muy bonito. Pero tiene un problema muy gordo. Durante una parte del ciclo el aire en superficie se calienta como a 0,2ºC / década. Durante la otra parte del ciclo se calienta como a 0ºC / década (no se calienta). O pon si acaso muy poquito, dependiendo de quién y dónde lo mida. Pero la teoría del miedo dice que se tiene que calentar a 0,21ºC en ausencia de ciclos. Y si los ciclos duran lo mismo (tiene pinta) y en una mitad tienes 0,2 de calentamiento y en la otra tienes no calentamiento, el resultado es la mitad de lo que predecían cuando no aceptaban los ciclos.
Y si le quitas la mitad del calentamiento a la teoría del miedo, te quedas con una estimación central de 3,2ºC / 2 = 1,6ºC de sensibilidad climática, o calentamiento por doblar el CO2, o calentamiento esperable a fin de siglo. Que es la misma sensibilidad que calculan Lewis y Curry, a los que insultan como negacionistas, herejes, y criminales contra la humanidad. Porque es muy difícil sostener que con esa sensibilidad climática el CO2 sea un problema.
No hay más.
- Lo que pasa mas halla de los 2000mts es despreciable para las escalas de tiempo que nos interesa ,esto ( ya te lo dije mas arriba )
Y lo que pasa debajo de los 700 también. Si queires que sea El Niño / La Niña lo que produce La Pausa, entonces el Calentamiento Global (1975 - 1998) tuvo contriibución de El Niño / La Niña. Y si durante La Pausa ese ciclo se lleva casi todo el "calentamiento antropogénico", entonces la fuerza de ese calentamiento es igual a la del ciclo. Y el Calentamiento Global Acojonante no era todo antropogénico, sino sólo la mitad.
Trenberth, primer enlace:
- “The picture emerging is one where the positive phase of the PDO from 1976 to 1998 enhanced the surface warming somewhat by reducing the amount of heat sequestered by the deep ocean, while the negative phase of the PDO is one where more heat gets deposited at greater depths, contributing to the overall warming of the oceans but cooling the surface somewhat.
No puedes jugar a todo. Bueno, es lo que hacen los alarmistas, pero es trampa. Si el "calor perdido" va al fondo del mar, entonces es como si hubiera desaparecido, para lo que nos importa. Y si el calor de La Pausa que no hay está en el juego El Niño / La Niña (que lo suelen medir hasta los 350 metros), entonces el efecto del CO2 es como la mitad de lo que dicen los modelos que no contaban con La Pausa.
- Ahora esto es un ciclo y el proceso se invertirá inevitablemente , la capa superior se volverá menos eficiente en transportar energía hacia las capas profundas ,como consecuencia esta se calentara mucho mas y la energía que antes iba a parar a las capas profundas se quedara en superficie calentando la atmósfera en el proceso..
Muy bonito. Pero tiene un problema muy gordo. Durante una parte del ciclo el aire en superficie se calienta como a 0,2ºC / década. Durante la otra parte del ciclo se calienta como a 0ºC / década (no se calienta). O pon si acaso muy poquito, dependiendo de quién y dónde lo mida. Pero la teoría del miedo dice que se tiene que calentar a 0,21ºC en ausencia de ciclos. Y si los ciclos duran lo mismo (tiene pinta) y en una mitad tienes 0,2 de calentamiento y en la otra tienes no calentamiento, el resultado es la mitad de lo que predecían cuando no aceptaban los ciclos.
Y si le quitas la mitad del calentamiento a la teoría del miedo, te quedas con una estimación central de 3,2ºC / 2 = 1,6ºC de sensibilidad climática, o calentamiento por doblar el CO2, o calentamiento esperable a fin de siglo. Que es la misma sensibilidad que calculan Lewis y Curry, a los que insultan como negacionistas, herejes, y criminales contra la humanidad. Porque es muy difícil sostener que con esa sensibilidad climática el CO2 sea un problema.
No hay más.
 Toda la chorrada de que ese calor que imaginan “escondido en el mar” es que, para que fuera un problema, el calor tendría que tener un sistema para volver al aire. Y no lo tiene. Una vez igualadas las temperaturas (en +0,001ºC), el calor no se mueve.
Otra supocicion que es falsa , las temperaturas nunca estuvieron igualadas con la atmósfera , y probablemente no lo estarán nunca, en la medida que siga existiendo un imbalance energético en el planeta,,,es decir mientras entre al planeta mas energía de la que sale , por el aumento incesante de los GHGs..
No entiendes nada. O el aire está pasando calor al océano (el "calor perdido) o no está. Si le está pasando calor (o más calor) solo lo puede hacer aumentando la temperatura, y perdiendo esa temperatura según le pasa el calor. Al la misma temperatura no le puede pasar más calor (el nuevo del "calentamiento global").
El sistema para que el calor en el mar vuelva al aire es por las corrientes oceánicas , por supuesto este no volverá TODO , sera una parte de este..
Si crees que diciendo corrientes oceánicas has dicho algo, en plan juego de manos, te equivocas. Y las corrientes oceánicas que pueden calentar el aire no son del "océano profundo", que es de lo que hablamos.
Otra falsedad es suponer que el calor la transmision de calor es unidireccional es decir que es siempre el aire el que se calienta primero y este despues le transmite la energia al mar , eso no es verdad, tambien pasa en sentido contrario.. Lo que quiero decir es que no todo el calor que contiene actaulemtente el mar vino de la atmosfera , y no todo el calentamiento de la atmosfera vino del mar , pasan las dos cosas al mismo tiempo , Y en verdad pasa mas de mar a atmósfera que de atmósfera a mar ( si lo medimos por cuanta energía aporta cada uno )
Problema. Yo no he dicho lo que afirmas. Cuando quieres citar, sabes citar. Y cuando quieres hacer trampas, te olvidas. Eres un primor.
Nunca he dicho que la transmision de calor es unidireccional es decir que es siempre el aire el que se calienta primero y este despues le transmite la energia al mar. Eso solo es lo necesario para la teoría alarmista de que el calor está pasando del aire al océano, y por eso el aire no se calienta. Pero no es necesario que ocurra siempre (yo creo que no ocurre casi nunca)
Resumiendo. No puedes entender el argumento si no distingues lo que digo yo, de lo que dicen los alarmistas estilo Trenberth. Yo digo que Trenberth esta diciendo chorradas, ¿entiendes?
En resumen. Si dicen que La Pausa no es cierta porque el calor se ha “escondido en el fondo del mar”, están diciendo una chorrada. Porque ese calor se ha perdido para siempre — a todos los efectos que nos pueden interesar.
Falso , primero que todo ,la energia no se pierde para siempre .. simplemente , queda alamcenada muchooo tiempo ,de cientos hasta 1000 años , esto es el caso de el calor que va a parar al océano abisal ( el mas profundo) pero resulta que muy poca ( por no decir nada ) de esa energía va a parar alli en escala de decadas a siglos , pero en las escalas de tiempo que nos importan , la mayor parte de la energía queda almacenada en la superficie del mar .. en las primeras capas 100 mts a 700mts y hasta los 2000mts . mas abajo es despreciable. La energia almacenada en estas capas pueden volver ( en parte ) a la atmosfera , por supuesto menos energia podra liberarse a la atmosfera cuando mas profunda sea la capa ..
Primero ¿Tienes algún problema especial para comprender la expresión "a efectos prácticos"? ¿Necesitas un dibujito?
Segundo. ¿Tienes algún problema especial en entender que no soy yo el que dice que el calor se ha ido durante estos 15 años de La Pausa al fondo del mar, sino algunos alarmistas muy notables como Trenberth? He proporcionado el enlace. He dicho "océano profundo", según tesis alarmista. Estás contestando que es falso que lo que dice Trenberth es un chorrada, y lo que dice Trenberth te parece imposible. ¿Y cuál es la diferencia entre chorrada e imposible, si puede saberse? ¿Como puede ser falso que sea una chorrada (eso dices) pero verdadero que sea imposible (eso dices, también). ¿Todavía no has comprendido los problemas que tienes para entender algo muy sencillo? ¿Y si no eres capaz de entender eso, quieres entender la discusión del "calentamiento global"?
Toda la chorrada de que ese calor que imaginan “escondido en el mar” es que, para que fuera un problema, el calor tendría que tener un sistema para volver al aire. Y no lo tiene. Una vez igualadas las temperaturas (en +0,001ºC), el calor no se mueve.
Otra supocicion que es falsa , las temperaturas nunca estuvieron igualadas con la atmósfera , y probablemente no lo estarán nunca, en la medida que siga existiendo un imbalance energético en el planeta,,,es decir mientras entre al planeta mas energía de la que sale , por el aumento incesante de los GHGs..
No entiendes nada. O el aire está pasando calor al océano (el "calor perdido) o no está. Si le está pasando calor (o más calor) solo lo puede hacer aumentando la temperatura, y perdiendo esa temperatura según le pasa el calor. Al la misma temperatura no le puede pasar más calor (el nuevo del "calentamiento global").
El sistema para que el calor en el mar vuelva al aire es por las corrientes oceánicas , por supuesto este no volverá TODO , sera una parte de este..
Si crees que diciendo corrientes oceánicas has dicho algo, en plan juego de manos, te equivocas. Y las corrientes oceánicas que pueden calentar el aire no son del "océano profundo", que es de lo que hablamos.
Otra falsedad es suponer que el calor la transmision de calor es unidireccional es decir que es siempre el aire el que se calienta primero y este despues le transmite la energia al mar , eso no es verdad, tambien pasa en sentido contrario.. Lo que quiero decir es que no todo el calor que contiene actaulemtente el mar vino de la atmosfera , y no todo el calentamiento de la atmosfera vino del mar , pasan las dos cosas al mismo tiempo , Y en verdad pasa mas de mar a atmósfera que de atmósfera a mar ( si lo medimos por cuanta energía aporta cada uno )
Problema. Yo no he dicho lo que afirmas. Cuando quieres citar, sabes citar. Y cuando quieres hacer trampas, te olvidas. Eres un primor.
Nunca he dicho que la transmision de calor es unidireccional es decir que es siempre el aire el que se calienta primero y este despues le transmite la energia al mar. Eso solo es lo necesario para la teoría alarmista de que el calor está pasando del aire al océano, y por eso el aire no se calienta. Pero no es necesario que ocurra siempre (yo creo que no ocurre casi nunca)
Resumiendo. No puedes entender el argumento si no distingues lo que digo yo, de lo que dicen los alarmistas estilo Trenberth. Yo digo que Trenberth esta diciendo chorradas, ¿entiendes?
En resumen. Si dicen que La Pausa no es cierta porque el calor se ha “escondido en el fondo del mar”, están diciendo una chorrada. Porque ese calor se ha perdido para siempre — a todos los efectos que nos pueden interesar.
Falso , primero que todo ,la energia no se pierde para siempre .. simplemente , queda alamcenada muchooo tiempo ,de cientos hasta 1000 años , esto es el caso de el calor que va a parar al océano abisal ( el mas profundo) pero resulta que muy poca ( por no decir nada ) de esa energía va a parar alli en escala de decadas a siglos , pero en las escalas de tiempo que nos importan , la mayor parte de la energía queda almacenada en la superficie del mar .. en las primeras capas 100 mts a 700mts y hasta los 2000mts . mas abajo es despreciable. La energia almacenada en estas capas pueden volver ( en parte ) a la atmosfera , por supuesto menos energia podra liberarse a la atmosfera cuando mas profunda sea la capa ..
Primero ¿Tienes algún problema especial para comprender la expresión "a efectos prácticos"? ¿Necesitas un dibujito?
Segundo. ¿Tienes algún problema especial en entender que no soy yo el que dice que el calor se ha ido durante estos 15 años de La Pausa al fondo del mar, sino algunos alarmistas muy notables como Trenberth? He proporcionado el enlace. He dicho "océano profundo", según tesis alarmista. Estás contestando que es falso que lo que dice Trenberth es un chorrada, y lo que dice Trenberth te parece imposible. ¿Y cuál es la diferencia entre chorrada e imposible, si puede saberse? ¿Como puede ser falso que sea una chorrada (eso dices) pero verdadero que sea imposible (eso dices, también). ¿Todavía no has comprendido los problemas que tienes para entender algo muy sencillo? ¿Y si no eres capaz de entender eso, quieres entender la discusión del "calentamiento global"?
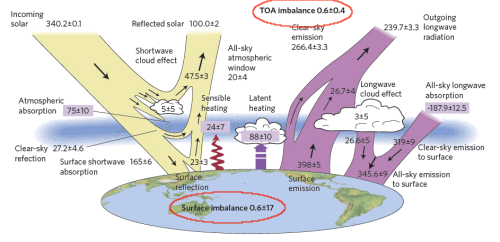 Trenberth, enlace proporcionado:
- As the deep ocean waters have slowly warmed they have taken heat from the upper ocean which has then cooled the atmosphere. This is the cause of the apparent hiatus in global warming that has manifested itself as a halt in the rise in global mean atmospheric temperatures seen in the second half of the 20th century.
Nadie ha medido ese calentamiento del océano profundo. Pero podemos calcular teóricamente cuánto se hubiera calentado el mar profundo si todo el calor que falta por La Pausa se hubiera ido allí.
Y una forma de calcularlo es:
- En el aire, ese "calor perdido" debería de producir 3,2ºC de aumento de temperatura por siglo, según la teoría calentóloga.
- Si ese calor que falta se estuviera yendo al fondo del mar, ¿cuanto podría calentar el fondo del mar?
Vamos a simplificar, y usar sólo "fondo del mar" en vez de el mar completo. La mitad inferior. Así no te mareas con las corrientes y con la estratificación. Y es lo que dice Trenberth: "deep ocean".
- Como la capacidad calorífica de la mitad inferior del mar será aproximadamente 500 veces superior a la de la atmósfera (como la mitad del mar completo), el mismo calor que calentaría la atmósfera en 3,2ºC al cabo de un siglo, calentaría el fondo del mar en 3,2 / 500 = 0,006ºC.
Ese es un calentamiento que no le puede preocupar a nadie. Ni mucho, ni poco, ni nada. Y ahora imagina tus famosos corrientes. Una corriente que proporciona aguas profundas a la superficie. ¿Me puedes contar cuánto puede calentar la superficie una corriente que ha aumentado su temperatura en 0,006ºC? ¡Pues exactamente 0,006ºC! Y sólo en el lugar en donde ocurre esa corriente.
Por supuesto, esto parte de una asunción que no está garantizada. Que el calor "perdido" que habría ido al mar profundo se reparte bien, y rápido. Y eso sin duda lleva su tiempo. Pero imagina lo que tendría que ocurrir para la propuesta de que el calor se esconde en el mar, y 20 años más tarde sale para comernos.
Trenberth:
- Decadal Oscillations (or PDOs) drive alternate 20-plus year cycles of upper ocean warming and cooling which also involve heat being exchanged with the atmosphere.
¿Cómo podría hacer eso? Tendría que esconderse en forma de una masa de agua caliente a más de 2.000 metros, o varias de esas masas, que mantienen durante 20 años una fuerte diferencia de temperatura con el agua que la rodea, y 20 años después esa misma masa (o masas) afloran a la supericie, a devolver el calor que habían escondido. O sea, el calor no estaría escondido "en el océano profundo", sino en un "almacén" muy especial dentro del océano profundo. O varios. He conocido películas de terror mucho más verosímiles. Y se podría sugerir que busquen esos almacenes tan prodigiosos antes de intentar aterrorizarnos con ellos.
Y ese es el problema del calor "escondido en el fondo del mar". Que no existe ningún mecanismo verosímil para sacarlo de ahí ... de una forma que alguien lo pueda notar.
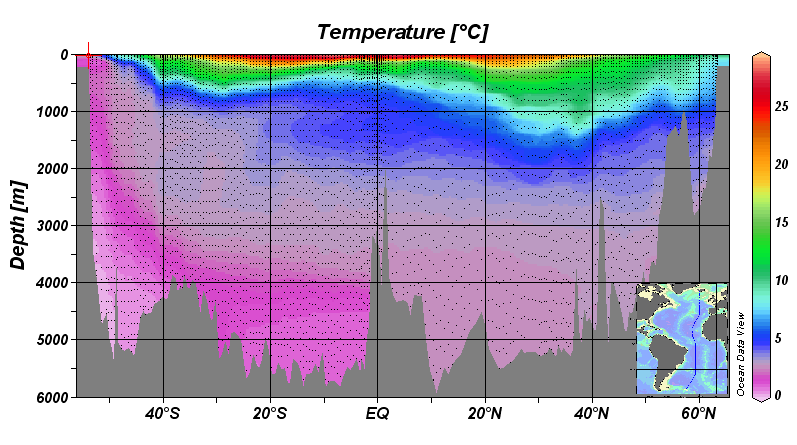
Hablando del mar profundo, esta es una imagen mejor que la anterior. Clic para aumentar.
Trenberth, enlace proporcionado:
- As the deep ocean waters have slowly warmed they have taken heat from the upper ocean which has then cooled the atmosphere. This is the cause of the apparent hiatus in global warming that has manifested itself as a halt in the rise in global mean atmospheric temperatures seen in the second half of the 20th century.
Nadie ha medido ese calentamiento del océano profundo. Pero podemos calcular teóricamente cuánto se hubiera calentado el mar profundo si todo el calor que falta por La Pausa se hubiera ido allí.
Y una forma de calcularlo es:
- En el aire, ese "calor perdido" debería de producir 3,2ºC de aumento de temperatura por siglo, según la teoría calentóloga.
- Si ese calor que falta se estuviera yendo al fondo del mar, ¿cuanto podría calentar el fondo del mar?
Vamos a simplificar, y usar sólo "fondo del mar" en vez de el mar completo. La mitad inferior. Así no te mareas con las corrientes y con la estratificación. Y es lo que dice Trenberth: "deep ocean".
- Como la capacidad calorífica de la mitad inferior del mar será aproximadamente 500 veces superior a la de la atmósfera (como la mitad del mar completo), el mismo calor que calentaría la atmósfera en 3,2ºC al cabo de un siglo, calentaría el fondo del mar en 3,2 / 500 = 0,006ºC.
Ese es un calentamiento que no le puede preocupar a nadie. Ni mucho, ni poco, ni nada. Y ahora imagina tus famosos corrientes. Una corriente que proporciona aguas profundas a la superficie. ¿Me puedes contar cuánto puede calentar la superficie una corriente que ha aumentado su temperatura en 0,006ºC? ¡Pues exactamente 0,006ºC! Y sólo en el lugar en donde ocurre esa corriente.
Por supuesto, esto parte de una asunción que no está garantizada. Que el calor "perdido" que habría ido al mar profundo se reparte bien, y rápido. Y eso sin duda lleva su tiempo. Pero imagina lo que tendría que ocurrir para la propuesta de que el calor se esconde en el mar, y 20 años más tarde sale para comernos.
Trenberth:
- Decadal Oscillations (or PDOs) drive alternate 20-plus year cycles of upper ocean warming and cooling which also involve heat being exchanged with the atmosphere.
¿Cómo podría hacer eso? Tendría que esconderse en forma de una masa de agua caliente a más de 2.000 metros, o varias de esas masas, que mantienen durante 20 años una fuerte diferencia de temperatura con el agua que la rodea, y 20 años después esa misma masa (o masas) afloran a la supericie, a devolver el calor que habían escondido. O sea, el calor no estaría escondido "en el océano profundo", sino en un "almacén" muy especial dentro del océano profundo. O varios. He conocido películas de terror mucho más verosímiles. Y se podría sugerir que busquen esos almacenes tan prodigiosos antes de intentar aterrorizarnos con ellos.
Y ese es el problema del calor "escondido en el fondo del mar". Que no existe ningún mecanismo verosímil para sacarlo de ahí ... de una forma que alguien lo pueda notar.
Hablando del mar profundo, esta es una imagen mejor que la anterior. Clic para aumentar.
