Reto matemático a los alarmistas del clima (100.000 $)
El reto, 100.000 dólares, es para que demuestren, estadísticamente, que hay un Calentamiento global Acojonante. En palabras de Doug Keenan, que es quien ofrece el premio de 100.000 $:
En esencia, el premio se concederá a cualquiera que pueda demostrar por análisis estadístico, que el incremento en la temperatura global probablemente no se debe a una variación natural aleatoria.En cristiano, viene a decir que una cosa es observar un calentamiento, y otra muy distinta es poder decir que ese calentamiento tiene algún significado digno de mención. ¿Pueden decirlo? Keenan afirma que no. Y pretende demostrárselo con una apuesta / premio al caballero que lo consiga.
Vamos a hacer un pequeño desvío para explicarlo. Imagina que ves esta serie de datos:
En principio ves una clara subida. Pero te interesa saber lo que va a pasar en adelante. ¿Va a seguir subiendo? Depende de cómo se hayan producido los datos que ves. Puede ser un proceso “aleatorio”, en el que lo mismo podían subir que bajar, pero ha ocurrido que subían – lo mismo que podía haber ocurrido que bajaran. O puede ser un proceso “tendencioso”, donde lo que se puede esperar es que los datos vayan en ascenso. Digamos que unos dados “sin trampa” serían un proceso aleatorio, y unos dados “cargados” serían un proceso con tendencia. Si son dados sin trampa, a largo plazo esperas que no se separen mucho del cero. Si son “tendenciosos”, esperas que los datos a largo plazo sigan esa tendenciosidad.
Si quieres entender esa serie, es muy diferente si ha salido con tres tiradas de dados o tres tiradas de monedas.
Por ejemplo, con monedas los valores podrían ser cara = +3; cruz = -3. Y cada tirada la sumas al valor anterior. Han salido tres caras. La probabilidad de tres caras seguidas es un 12,5%. No puedes apostar mucho a que las monedas estén cargadas, o sean “tendenciosas”. El resultado de la serie no es muy improbable para unas monedas sin “cargar”, sin tendencia.
Si el gráfico se ha producido con dados, de forma que el 1 vale -3, el 2 vale -2 … y el seis vale +3, has tenido tres seises seguidos. La probabilidad de esa tirada es un poco menos del 0,5%.
Cambia mucho. No sabes cómo se ha producido la serie. Pero si asumes que se sale de monedas no es improbable que sea aleatoria; y si asumes que es con dados, resulta 25 veces más improbable que no esté cargada, que no tenga una tendencia.
Cómo interpretes la serie depende de qué asunciones hagas sobre cómo se produce. Y esas asunciones pueden ser de dos tipos. Físicas, si conoces cómo funciona físicamente el sistema; o matemáticas, analizando las propiedades estadísticas de los datos que tienes.
Y ahora podemos ira a la apuesta de Doug Keenan. Los alarmistas del clima tienen esta serie de temperatura global.

Y dicen que pueden demostrar, con puro análisis estadístico, que la serie no es aleatoria. Que sale como de unos dados “cargados”, “tendenciosos”. La segunda parte, ya mirando el sistema físico, es concluir que lo único que puede producir esa “tendenciosidad” son las emisiones de CO2.
En realidad hay estudios estadísticos en un sentido y en otro; y una discusión de una oscuridad muy propia de la estadística. Y en este contexto, el reto y premio de Doug Keenan tiene bastante gracia.
Ha habido muchas afirmaciones sobre una evidencia observacional del calentamiento global alarmista. Yo he argumentado que todas esas afirmaciones se basan en análisis estadísticos inválidos. Algunos defienden la validez de esos análisis. Esa gente asegura, en particular, que pueden determinar, vía análisis estadístico, que la temperatura global está subiendo más delo que se podría esperar razonablemente de una variación natural aleatoria. No presentan un argumento que contradiga al mío, pero siguen con su afirmación en cualquier caso.Y les pide, premio mediante, que demuestren su capacidad de distinguir entre una serie aleatoria y otra con "tendenciosidad". Por el expediente de presentarles mil series temporales [-->], estadísticamente comparables a la de la temperatura global. Todas están creadas sin tendencia, por un proceso aleatorio. Y a algunas les ha añadido una tendencia, positiva o negativa, mayor que la que tiene la temperatura global (si interpretas que la tiene).
Reto: si decís que sois capaces de descubrir esa tendencia no aleatoria en la temperatura global, deberías ser capaces de averiguar a cuáles de mis series han sido generadas por un proceso con tendencia – que es mayor que la que aseguráis que tiene la temperatura global. Y si acertáis en 900 casos de los mil, señalando cuáles llevan tendencia y cuáles no, os doy 100.000 dólares.
Por curiosidad, para poderse hacer una idea, pongo un gráfico con las tres primeras series de Keenan.
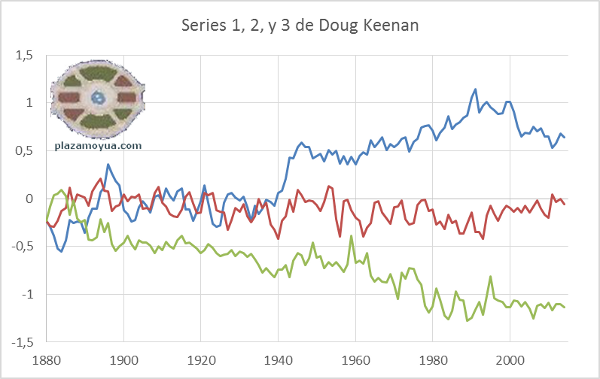
En sus propias palabras, y sin traducir – para no pervertir:
The file Series1000.txt contains 1000 time series. Each series has length 135 (about the same as that of the most commonly studied series of global temperatures). The series were generated via trendless statistical models fit for global temperatures. Some series then had a trend added to them. Each trend averaged 1°C/century—which is greater than the trend claimed for global temperatures. Some trends were positive; others were negative.Es interesante la explicación completa de Doug Keenan del asunto que hay detrás de la apuesta. Y de las inconsistencias del último informe del IPCC: --A prize of $100 000 (one hundred thousand U.S. dollars) will be awarded to the first person, or group of people, who correctly identifies at least 900 series: i.e. which series were generated by a trendless process and which were generated by a trending process.
Fuentes.
Bishop-Hill:
Doug Keenan, con relato de sus discusiones con los estadísticos el Met Office:
--Añadido (un día después). Unos ejemplos gráficos más para captar la idea. Algunas de las series de Keenan junto a la temperatura global (HadCrut4, siempre en negro).
Las tres primeras, sólo por ser las tres primeras.
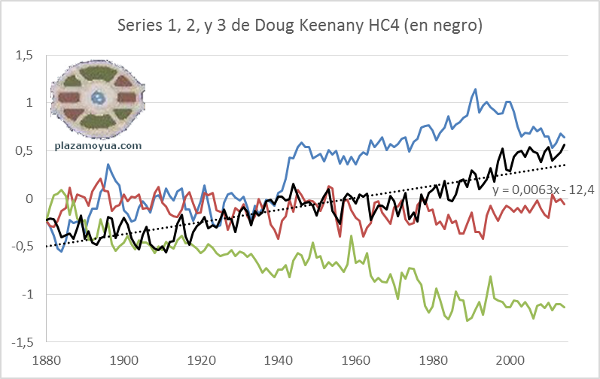
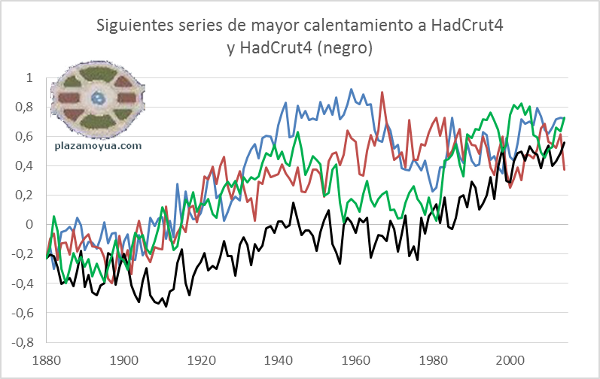
Las tres de mayor calentamiento de Keenan, con HadCrut4 (negro).
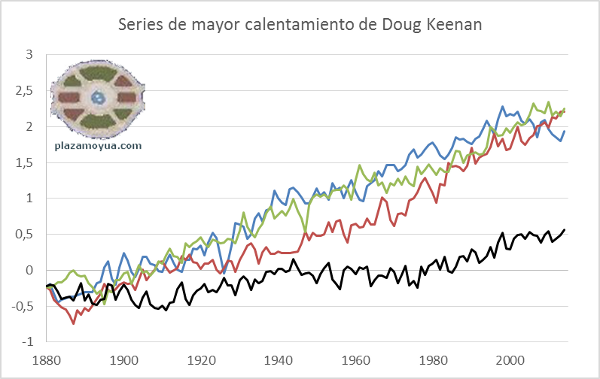
Las dos de tendencia más similar a HadCrut4 y HadCrut4 (en negro). Una es un pelín más caliente, y la otra un pelín menos.
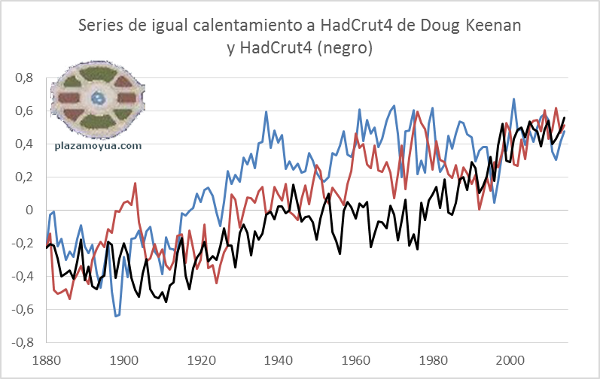
Entre las mil series de Keenan, hay 200 que tienen más calentamiento que HadCrut4. Estas son las tres siguientes a la que acabamos de ver arriba.
Y esta es muy bonita. Las tres más extremas de calor, y de frío; y las dos más parecidas a HadCrut4. Con HAdCrut4 en negro.
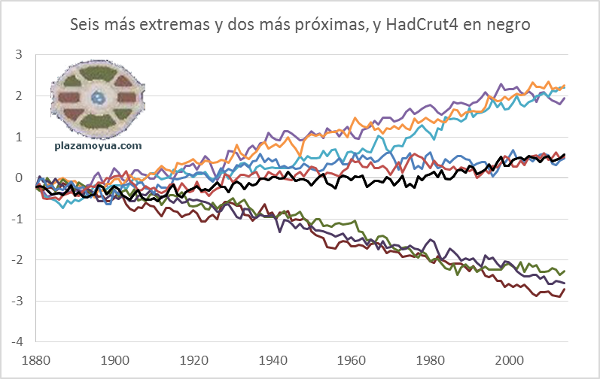
La primera impresión es que Doug Keenan lo ha hecho muy bien. Si no fuera por haberla puesto en negro (y saberlo), no habría manera de distinguir la serie de temperatura real de las generadas por su sistema. Si ha conseguido, por ejemplo, que un buen porcentaje de las 200 que muestran más calentamiento que HadCrut4 estén generadas aleatoriamente (sin añadirles tendencia), estaría planteando un ejercicio interesantísimo.
O las aciertan, o no las aciertan. Y si no las aciertan, no tienen un sistema estadístico para distinguirlas. Y en ese caso, no pueden decir por medios estadísticos que el calentamiento global no sea una "variabilidad natural aleatoria".
Podrían alegar que lo pueden decir por un conocimiento del sistema físico. Pero esa es otra cuestión diferente, que a su vez plantea no pocos problemas. Y que tiene un carro de literatura científica en contra bastante considerable. Literatura delicada, porque es con proxys. Pero es el "mejor conocimiento que hay", valga lo que valga.
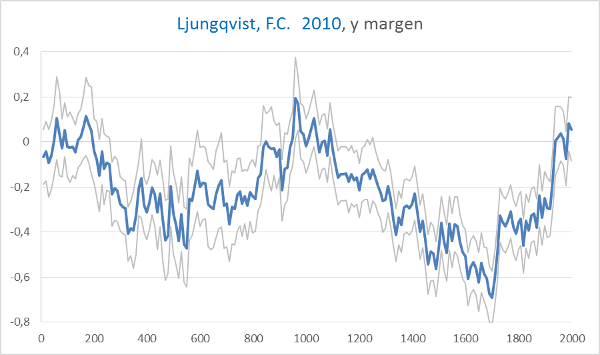
Por ejemplo, Ljungqvist.
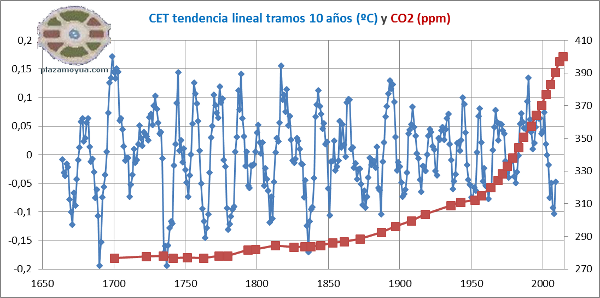
Por ejemplo, CET. Tendencia de temperatura en Inglaterra Central en tramos de 10 años.
Por ejemplo, Kobashi 2011 sobre Groenlandia Central.
De las anteriores observaciones deducimos que la temperatura en Groenlandia Central no ha excedido el rango de la variabilidad natural.
