A Peter Pan le dicen

Viene de –>

Me ha encantado saber qué líneas de tendencia valen, y cuales no, calculando su significación estadística según que la tendencia sea mayor o menor que la variabilidad de los datos. Lo que pasa es que voy a empezar a cagarme en la estadística más que en los economistas, que ya es decir.

Por ejemplo, veo en le web del German Advisory Council on Global Change [–>], este gráfico:

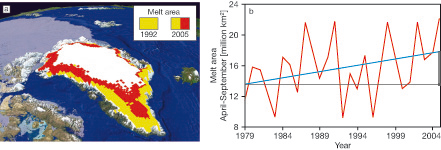
Y me da la impresión de que la tendencia es mucho menor que la variabilidad. Según Peter Pan hay que llamarles inmediatamente para decirles que esa gráfico no vale. Te doy el email si me prometes contarme la respuesta.

Otro más que no vale:

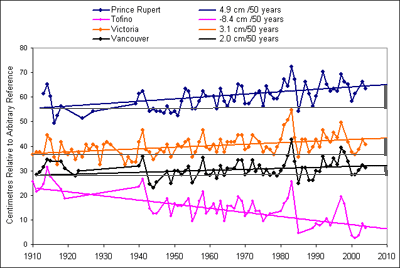
Hay que llamar al Ministry of Environment de Canadá, pero ya [–>].

Pero es que además eso me plantea un problema teórico. Imagina una serie de datos a lo largo del tiempo representados en un eje XY. 1.000 años. Los valores oscilan entre +5 y -5. Y haces una regresión lineal y la tendencia te da 0 patatero. Luego la tendencia es 0 patatero. ¿Es mayor o menor que la variabilidad? Conclusión: en una serie de variabilidad = 10, no tiene significación estadística cualquier tendencia menor a 10. Y nos quedamos sin saber la tendencia de esos datos. ¿Esa es la idea? Mil años. Los datos oscilando constante y armoniosamente alrededor de cero, pero no sabemos la tendencia. No hay tendencia. Si es que no somos nadie.

Pero no desesperes. Aun podemos buscar modo de dar significado a ese período “no estadísticamente significativo” 2005 - 2009. Si los doce años 1993 - 2005 son significativos, mientras la tendencia o la variabilidad no tengan cambios espectaculares, serán igualmente singificativos los períodos …

1994 - 2006
1995 - 2007
1996 - 2008
1997 - 2009

¿Qué pasa con la tendencia en esos períodos? Pues es fácil de ver lo que pasa "a ojo": nivel_mar_uc_tisdale-raya

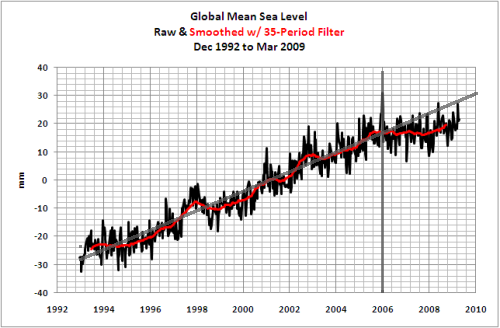
El primer período acaba en 2006. A partir de ahí pilla un año de la derecha, que siempre es un año que queda por debajo de la raya, y suelta un año de la izquierda. Cada vez tienes un año más por debajo de la raya. Y la raya, aunque el origen está puesto a huevo, representa la inclinación de 3,2 mm / año del período. Es paralela a la línea de tendencia.

Y por si facilita la visión de la jugada, pongo un cuadro con las medias anuales de los mismos datos. muy útil para ver como baja la media de esos sucesivos períodos de 12 años.

nivel_mar_anhos_tisdale

Así que según se desplazan a la derecha los sucesivos períodos, cada período de 12 años va teniendo una tendencia menor. Empezará en 3,5, y acabará en 3,1.

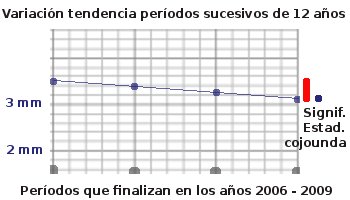
¿Que está haciendo la tendencia “estadísticamente significativa”? ¡¡Disminuir de año en año!! Con lo que le hemos dotado de significación a lo que no parecía tenerla. ¿Vale?

Advertencia: Evidentemente no he hecho el cálculo de la tendencia de los cuatro períodos. Pero sí recuerdo que la tendencia, según la UC, era 3,4 en 2007, 3,3 en 2008, y 3,2 desde mayo 2009 (el “release” 3). Así que no le puede andar muy lejos. Ah, y si tienes dudas con las gráficas 3 y 4, los datos son los que vienen en la web de nivel del mar de la Universidad de Colorado. La conoces.

–

Veamos lo que ha pasado en un plazo un poco más “estdísticamente significativo” (puesto que la diferencia entre la tendencia y variabilidad es mejor que en tu caso 1993 - 2005).

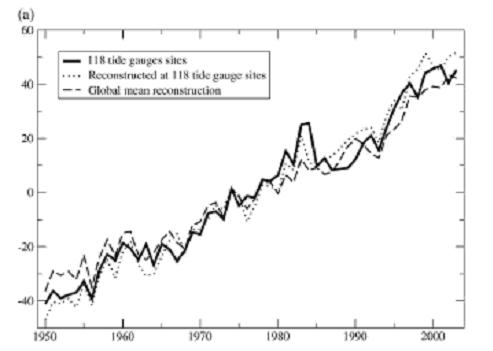
Es la figura de Berge-Nguyen 2007 a pelo, sin rayas. Solo mediciones clásicas, sin satélites. ¿Tú ves ahí una aceleración según suben los niveles de carbono? Yo tampoco. Aunque los dos sabemos que si Mann y Rahmstorf se ponen manos a la obra, nos sacan un palo de hockey en un pispás.

Sigamos viendo. Con una raya de tendencia. La inclinación es la que da la obra, 1.5 mm/ año, y he puesto el origen “a ojímetro”, pero sirve como ayuda visual. Y señalo el año 1993, calve en esta historia. Es el año en que empieza esa supuesta “aceleración estadísticamente significativa”.

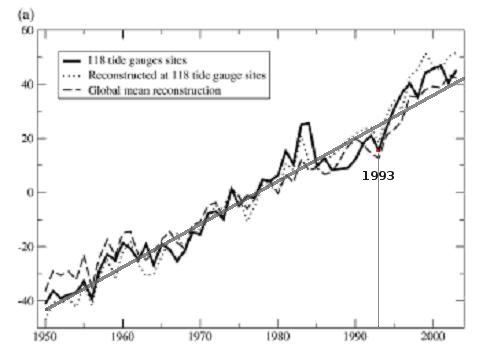
¿Ande está la “aceleración”? Solo la puedes ver si mezclas peras con manzanas. O sea, si mezclas exclusivamente el periodo 1993 - 2005 con el 1950 - 2005. 12 años contra 55. Pero lo que hay que hacer es comparar esos 12 años contra otros perídos similares, para ver si hay algo raro en ellos. Yo no lo veo. Que venga Rahmstorf. Lo que veo es como los datos oscilan a uno y otro lado de la tendencia de 1,5 mm, con una máxima separación entre 1983 y 1985, pero nada como para asustar. Unas veces toca por arriba, y otras veces toca por abajo. Eso es todo lo que veo.

Pero imaginemos que nos trasladamos a 1985 y no sabemos los datos que habrá más adelante. Y miramos la tendencia reciente, “estadísticamente significativa”. Y la dibujamos. A ojímetro sí, pero te juego una cena que no muy lejos de las matemáticas:

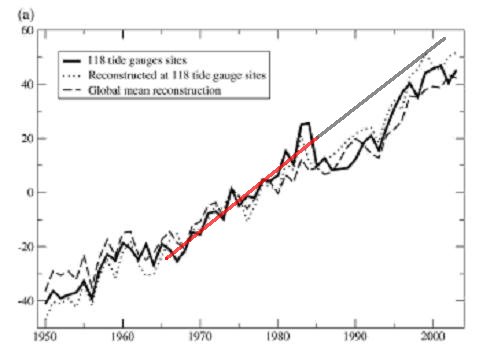
Y ahora, de nuevo en 2009, vemos que los datos posteriores a 1985 se han mantenido (todos) por debajo de la raya, en lugar de cruzarla, como solían. Y nos vamos a los periódicos diciendo: ¡Se ha desacelerado! Y además es “estadísticamente significativo”.

¿A que no es serio? Pues es lo mismo.

Bien, pues ahora que creo haber explicado, aunque sea torpemente, mis dificultades, te pediría que me expliques qué está pasando, y por qué debemos de estar tan preocupados.

[caption id=“attachment_5218” align=“aligncenter” width=“423” caption=“Jerejeva et al 2007”] Jevrejeva_sea_level [/caption]

–

–

Añadido (noticia): Como tenemos un poco de “peer-reviewed obsession”, tal vez merezca la pena poner esta noticia que da Pielke (sr.):

Stay tuned also for at least two peer reviewed papers which are quantitatively analyzing, using Anthony’s data (Anthony Watts), the impact of the poor sitings of the HCN sites on the long term surface temperature trends and anomalies. [-->]

PeterPan 2009-07-23 09:17:10
Lo que comento de la variabilidad y la tendencia es un indicativo visual intuitivo, pero no es definitivo. Para saberlo con certeza habría que calcular el error de la tendencia según la definición de mínimos cuadrados. Ese error viene a indicar cuánto de estable es la tendencia. Es decir, cuánto varía la tendencia si quito o pongo unos pocos datos al principio, en medio o al final. Esta estabilidad suele venir determinada por la relación entre la tendencia y la amplitud de la variabilidad que he señalado antes, pero por ejemplo puede darse el caso que la variabilidad sea tan regular que, aunque quitemos unos datos, la tendencia siga siendo casi la misma a pesar de tener menor amplitud que la variabilidad. El error de la tendencia puede calcularse como indican en la página 11 de este documento (ver fórmula 13). Una vez calculado el error de la tendencia, podemos estimar la significancia ponderando tendencia y error (tendencia / error_tendencia). Aunque en los documentos técnicos suelen usar definiciones más afinadas de significancia (derivadas de t-student, p.ej.). La idea pues es que cuando tienes una tendencia estadísticamente significativa, esta no cambia sustancialmente por añadirle o quitarle unos pocos datos. De todos modos, aunque tuvieras razón en que tomando tendencias significativas variando levemente los años ésta varíe de 3,4 a 3,2, estamos dentro del margen de error de la tendencia detectada (3,2 +/- 0,4, esto es, entre 2,8 y 3,6), así que puede decirse que la tendencia detectada es la misma. En cualquiera de los casos seguimos muy por encima de las proyecciones del IPCC (1,9), que es de lo que estamos hablando. Es decir, el informe de Copenhague no está haciendo ninguna proyección a futuro, simplemente está evaluando si los datos ya observados se han ajustado a las proyecciones del anterior informe de síntesis (el del IPCC), y lo cierto es que están por encima ("are progressing faster tan was expected"). Saludos.
plazaeme 2009-07-23 09:39:23
Bueno, puedo estar de acuerdo si hacemos una correccion: progressing faster than we -or IPCC- thought Y con cinco precisiones. 1) El progressing carece de sentido, puesto que has medido entre un valle y una cresta de un ciclo (por lo que sabemos hasta el momento). Y te he mostrado lo que ocurre en ese caso, con el ejemplo de la medición hipotética en 1985. 2) El "we -or IPCC-" carece de sentido. Solo muestra que los modelos no valen -no saben lo que pasa- pero no que la conclusión final sea la suya, aumentada. 3) No hay forma, fuera de virguerías estadísticas no admitidas por los estadísticos no climáticos, de ver relación entre la subida del nivel del mar y el CO2. 4) No nos muestran un gráfico que no mezcle la tendencia de los mareógrafos y los satélites. ¿Como quedaría la cosa con solo mareógrafos? Cual es la diferencia de tendencia 1993 - 2005 entre mareógrafos y satélites? Yo no la he encontrado. Sospechoso. 5) Sí están haciendo proyecciones, pero sutilmente (engañosamente). Te dicen que los datos van por la raya máxima del IPCC y acaban hablando -sin explicar como- de un metro o más de subida para 2100. Que se corresponde con el caso máximo IPCC. Ergo ... Pero el caso es que la tendencia medida por los satélites, probablemente entre valle y pico de un ciclo, lleva a 32 cm para 2100, y no a más de un metro. ¿No es maravillosamente sutil? En caso contrario responde a la pregunta, y explícame por qué debemos preocuparnos.
PeterPan 2009-07-23 10:37:45
3) Pero sí crees que el nivel del mar varía en función de la temperatura, ¿no? 5) No es que los datos vayan por la raya máxima del IPCC, sino que están muy por encima de la raya máxima del IPCC. En cuanto a las proyecciones a futuro, éstas no se basan en esta tendencia reciente, sino en la creencia de que las temperaturas seguirán aumentando. La subida de nivel debida a la expansión térmica del agua es fácil de calcular con física teórica. Quedaría el aporte del deshielo, para lo cual se basan sobre todo en correlaciones históricas entre temperatura y nivel del mar halladas mediante diferentes aproximaciones. Saludos.
plazaeme 2009-07-23 12:54:02
3) Claro; no lo creo; lo sé. Bueno, no depende de la temperatura, sino del calor del mar. ¿Y qué? 5) Depende. Depende de qué raya porque al IPCC le gusta hacer muchas rayas (y alguna acertará). Mira, según tus amigos de Real Climate, ... "Note that the observed sea level rise tends to follow the uppermost dashed line of the IPCC scenarios, namely the one “including land ice uncertainty" http://www.realclimate.org/index.php/archives/2007/03/the-ipcc-sea-level-numbers/ La segunda figura. En cuanto a las proyecciones a futuro, éstas no se basan en esta tendencia reciente, sino en la creencia de que las temperaturas seguirán aumentando. Claro, el perfecto argumento circular. El nivel del mar confirma el problema del CO2 (aunque las temperaturas no aumenten) y como el problema del CO2 hará aumentar las temperaturas, aumentaŕa el nivel del mar. Acojonante, macho. Sí, la expansión térmica del agua es muy fácil de calcular, claro. Lo que resulta es que si el CO2 estuviera metiendo calor en el sistema climático, estaría entrando calor en el mar, que es la gran reserva térmica del sistema (85%). Y, lástima, pero ese calor no está. /media/2009/06/dipuccio-2.jpg?w=350&h=306&h=306
PeterPan 2009-07-24 08:21:49
3) Nada, era sólo para centrarnos ;-) (de la temperatura de los océanos, sí). 5) Ya, sí, me refiero a por encima de lo proyectado por los modelos (como dicen en ese mismo artículo: "50% faster than models suggest"). De todos modos eso es del informe de 2001. En el de 2007 pasaron de considerar el aporte de las placas de hielo porque los modelos fallaban (así que bajaron la proyección de 88 cm a 59 cm). Curiosamente, sobre el tema de la aceleración, ese artículo de RC también dice: "the discrepancy could be considered not significant given the error ranges of observations and models. It is no proof that models underestimate future sea level rise. But it is at least a plausible possibility that the models may underestimate future rise". Lo que interpreto pues es que ellos también dicen que esa aceleración no tiene por qué mantenerse. No es un argumento circular: sabes que sube el CO2 y esperas que suban las temperaturas. Si suben las temperaturas, también esperas que suba el nivel del mar. Mides las temperaturas y suben (aire y mar). Mides el nivel del mar y sube. Simplemente confirma las expectativas, pero la creencia de que seguirán aumentando las temperaturas se basa en lo mismo que al principio; en que las emisiones continuarán, no en lo observado en el nivel del mar. Con este tema acabaríamos de nuevo hablando de períodos significativos... 😛 Saludos!
plazaeme 2009-07-24 10:02:28
Joé, tú, Peter Pan, si nos ponemos a discutir al pedo vamos a perder un tiempo que podríamos dedicar a cosas mucho más provechosas y/o interesantes. Te he hecho una pregunta bien clara: te pediría que me expliques qué está pasando, y por qué debemos de estar tan preocupados. Y tú me contestas varias cosas ... 1) the discrepancy could be considered not significant given the error ranges of observations and models. It is no proof that models underestimate future sea level rise. But it is at least a plausible possibility that the models may underestimate future rise no es prueba ... pero al menos hay una posibilidad verosímil de que los modelos hayan subestimado. Acojonante. Al menos hay una posibildad verosímil de que unos modelos que no han probado nada, hayan subestimado un problema, de momento imaginario. Pues a mi no me parece muy comparable al mensaje de Copenhague que tanto publicitas. Tampoco has contestado a casi ninguna de las otras preguntas, que me he molestado en numerar. Y cuando contestas, 2 de 5, sales por peteneras. P: 3- No hay forma, fuera de virguerías estadísticas no admitidas por los estadísticos no climáticos, de ver relación entre la subida del nivel del mar y el CO2. R: 3) Pero sí crees que el nivel del mar varía en función de la temperatura, ¿no? ¡Que sí, joé! Y del ciclo del agua en el sistema y la salida de la Pequeña Edad de Hielo. Pero la discusión es si el CO2 afecta el sistema climático, y cuanto. Y te he preguntado varias veces como ves esa afección en lo que sabemos de la subida del niver del mar. Aquí: /media/2009/07/sea_level_update_fig21.jpg O aquí: /media/2009/07/jevrejeva_sea_level1.jpg O en el cuadro que quieras donde se vea la subida del nivel del mar antes y despues de la aceleración fuerte de las emisiones de CO2. 5 - Vale el IPCC tiene muchos cuadros. La discusión relevante no es si va más o menos por encima de no sé cual de las hipótesis (escenarios) de no sé cual de los "releases" del IPCC. Son muchos, y en realidad me importa un pimiento si va por encima de este o por debajo de aquel. Lo que me importa es la relevancia que pueda tener el que vaya por encima de este o por debajo de aquel. Y la relevancia dependerá de la relevancia del modelo. Por lo que sabemos, ninguna relevancia. /media/2009/06/dipuccio-2.jpg No has contestado a ... 1) El progressing carece de sentido, puesto que has medido entre un valle y una cresta de un ciclo (por lo que sabemos hasta el momento). Y te he mostrado lo que ocurre en ese caso, con el ejemplo de la medición hipotética en 1985. 2) El “we -or IPCC-” carece de sentido. Solo muestra que los modelos no valen -no saben lo que pasa- pero no que la conclusión final sea la suya, aumentada. 4) No nos muestran un gráfico que no mezcle la tendencia de los mareógrafos y los satélites. ¿Como quedaría la cosa con solo mareógrafos? Cual es la diferencia de tendencia 1993 – 2005 entre mareógrafos y satélites? Yo no la he encontrado. Sospechoso. y a 3) y 5), por peteneras. Y sobro todo, no has contestado lo único que importa: te pediría que me expliques qué está pasando, y por qué debemos de estar tan preocupados. Saludos agotados. 😉
PeterPan 2009-07-24 12:46:16
Esta parte: “1) the discrepancy could be considered not significant given the error ranges of observations and models. It is no proof that models underestimate future sea level rise. But it is at least a plausible possibility that the models may underestimate future rise” Te la he puesto precisamente dándote la razón. Como he dicho antes: “Lo que interpreto pues es que ellos también dicen que esa aceleración no tiene por qué mantenerse”. Copenhague no hace ninguna proyección a futuro. Habla de algo observado hasta la actualidad. Las razones por las que no contesto a los demás se dividen en dos: A- No lo sé. Resulta que no soy el dios del cambio climático y no lo sé todo (nadie lo sabe). El que tú y yo no sepamos algo no sirve para demostrar nada. Así, tu pregunta: 4) ¿Cómo quedaría la cosa con solo mareógrafos? No lo sé. Si ves algún documento riguroso que realmente se moleste en hacer un análisis estadístico y en evaluar la consistencia y fiabilidad de cada uno (satélites Vs mareómetros), coméntanoslo, please. Yo haré lo mismo (ya he puesto que RC estima que la incertidumbre sobre las observaciones es suficientemente amplia como para que finalmente no esté tan arriba, que aunque no sea un trabajo riguroso, te da parte de razón en esto). Seguramente haya alguien que lo haya hecho, ¿por qué no se conoce? Esto es otra especulación: tú especulas sobre una conspiración mundial de los científicos para ocultar la verdad, yo creo que es porque la diferencia no será… significativa 🙂. En todo caso, eres tú el que inicia la conversación ilustrándonos sobre el cambio climático, así que las respuestas deberías tenerlas tú. Yo te digo que para analizar si ha cambiado una tendencia hay que evaluar la significancia del cambio, pero no entiendo por qué se supone que tengo que daros el cursillo completo de estadística. Y Como segunda razón, B- El artículo tuyo que yo comenté trataba de una cosa muy concreta: si los datos de los últimos 4 años del nivel del mar prueban que el nivel del mar no ha progresado más rápido de lo que proyectó del IPCC. ¿Crees que a raíz de eso podemos discutir toda la ciencia del cambio climático en una charlita de blog? No te voy a seguir el juego de ir dando saltos sucesivos de una cosa a otra y de argumento en argumento para que al final parezca como si todo fuese lo mismo y por tanto nada de nada estuviese claro. Las añadiduras y preguntas colaterales son off-topic y el tamaño de los mensajes crecería exponencialmente (ya son suficientemente largos como para dispersarnos tanto). Como tú bien dices, seguramente ambos (y los eventuales lectores) tenemos cosas más interesantes que hacer ;-) Pero en fin, echemos un ojo: 1) “has medido entre un valle y una cresta de un ciclo”. Esto es un cambio de argumento, no constaba ni en tu artículo inicial ni en mi comentario. Existe la posibilidad de que estés en lo cierto, pero hasta que no hagas un análisis estadístico con los datos o encuentres un documento en que lo hagan, no es más que una especulación. Para empezar, estás comparando peras con manzanas: el ruido y margen de error de los mareógrafos y los satélites es totalmente distinto, así que lo que en satélites es significativo puede no serlo en mareógrafos. Como ves, RC dice que lo medido con satélite tiene significancia, y que yo sepa Pielke no lo niega en su respuesta. 2) Si los datos muestran que los modelos fallan, muestran que fallan en un sentido muy concreto: infraestimando. Los datos no muestran por ningún lado que lo sobreestimen, así que esa conclusión de que falla para ambos lados no se apoya en ninguna evidencia. 3) No hay forma, fuera de virguerías estadísticas no admitidas por los estadísticos no climáticos, de ver relación entre la subida del nivel del mar y el CO2. Como he dicho antes, si pretendemos hablar del nivel del mar, la conexión es con la temperatura. La conexión CO2-temperatura puede ser muy interesante, pero es off topic y no podemos cubrirlo todo. Incluso para mostrar que la variación de T ha sido el factor determinante de la subida del nivel del mar durante el s. XX podríamos tirarnos páginas y páginas. And last but not least: te pediría que me expliques qué está pasando, y por qué debemos de estar tan preocupados Esto ya sí que es pretender cubrirlo todo (porque después de nivel del mar-tempertura vas a querer conectar temperatura-emisiones). No podemos abarcar más de 30 años de trabajo de especialistas (y encima pretendiendo profundizar tanto) en una pequeña charla entre cervezas ;-), simplemente podemos comentar detallitos. Pero ya sabes que a esa pregunta es a la que pretende responder el informe del IPCC, al que se puede acceder con diferente profundidad: Poca: http://www.ipcc.ch/pdf/assessment-report/ar4/syr/ar4_syr_spm.pdf Media: http://www.ipcc.ch/pdf/assessment-report/ar4/syr/ar4_syr.pdf Mucha: http://www.ipcc.ch/publications_and_data/publications_ipcc_fourth_assessment_report_wg1_report_the_physical_science_basis.htm http://www.ipcc.ch/publications_and_data/publications_ipcc_fourth_assessment_report_wg2_report_impacts_adaptation_and_vulnerability.htm Yo también estoy agotado. Salut!
plazaeme 2009-07-24 13:07:21
Copenhague no hace ninguna proyección a futuro. Habla de algo observado hasta la actualidad Copenhagen Synthesis Report Climate Change: Global Risk, Challenges and Decisions http://climatecongress.ku.dk/pdf/synthesisreport KEY MESSAGE 1: Climatic Trends Recent observations show that greenhouse gas emissions and many aspects of the climate are changing near the upper boundary of the IPCC range of projections. Many key climate indicators are already moving beyond the patterns of natural variability within which contemporary society and economy have developed and thrived. These indicators include global mean surface temperature, sea-level rise, global ocean temperature, Arctic sea ice extent, ocean acidification, and extreme climatic events. With unabated emissions, many trends in climate will likely accelerate, leading to an increasing risk of abrupt or irreversible climatic shifts. Ese es el mensaje. Y acabamos de ver en qué se sustenta. Gracias. Slds.
plazaeme 2009-08-03 07:37:57
Unos enlaces que explican lo falso de la canción de moda según el Copenhagen Sintesis Report: http://rankexploits.com/musings/2009/source-of-fishy-odor-confirmed-rahmstorf-did-change-smoothing/ Lucia: That is: the method Rahmstorf used has been known to be a very poor method for testing projections. Period. This has been known for eons. For this reason, few would bother to submit a peer reviewed paper on the subject because the discovery of how bad the method is not new. (Peer reviewed articles are supposed to present something new information. So, the the paper would, justifiably be rejected on the basis of simply rehashing widely known information.) http://landshape.org/enm/rahmstorf-2007-discredited/ Por otra parte: Peter Pan: And last but not least:
te pediría que me expliques qué está pasando, y por qué debemos de estar tan preocupados
Esto ya sí que es pretender cubrirlo todo (porque después de nivel del mar-tempertura vas a querer conectar temperatura-emisiones). No podemos abarcar más de 30 años de trabajo de especialistas (y encima pretendiendo profundizar tanto) en una pequeña charla entre cervezas ;-) , simplemente podemos comentar detallitos. Pero ya sabes que a esa pregunta es a la que pretende responder el informe del IPCC, al que se puede acceder con diferente profundidad. PM: No. No estamos juzgando los informes del IPCC, ni comentando detallitos. Estamos juzgando la pretensión del Copenhagen Sintesys Report de que la cosa está peor de lo que proponía el IPCC. Y no se sostiene. Por cierto, tu cita de literatura a favor de la tesis Copenhague es un poco curiosa. Aquí citas seis trabajos. De los seis, ... * el primero (Church y White) dice: If this acceleration remained constant then the 1990 to 2100 rise would range from 280 to 340 mm, consistent with projections in the IPCC TAR.. A mi no me suena a "peor de lo que pensábamos" (pensaba el IPCC) sino a "consistente con". * el segundo, tercero, cuarto y quinto, son el mismo, y es de 2001 (Cecile Cabanes, Anny Cazenave, Christian Le Provost). Difícilmente pueden decir que el nivel del mar es peor que la previsión del IPCC de 2007. * y el último (Holgate y Woolworth, del Proudman Oceanographic Laboratory) es de 2004. Y resulta que en su último trabajo de Hogate dice: The mean rate for the twentieth century calculated in this way is and the 1.67±0.04 mm/yr. The first half of the century (1904-1953) had a slightly sea higher rate (1.91±0.14 mm/yr) in comparison with the second half of the surface temperature century (1.42±0.14 mm/yr 1954-2003). http://meteo.lcd.lu/globalwarming/Holgate/sealevel_change_poster_holgate.pdf

<< Posterior	¿Que va a pasar con la temperatura?
Anterior >>	Peter Pan dice