Estadísticas de kindergarten para alarmistas del clima, y los diez años más calientes #nosvamosamorirtodos
Es que alucinas. Si tienen una “ciencia establecida”, una idea científica archi-corroborada por múltiples líneas de evidencia, y algo que si lo dudas te conviertes nada menos que en un “negacionista”, ¿se puede saber por qué cojones nos intentan engañar como si fuéramos niños de baba?
Ya hemos visto [–>] el intento de timo del récord imaginario de temperatura del año 2014, cuando sus propios números dicen que es más probable que no lo haya hecho. Organismos científicos como el instituto GISS, de la NASA, o la NOAA. Nada menos. Pero los divulgadores científicos se adornan todavía más. Porque los científicos les dan pie. Habréis visto muchas veces ya, lineas del tipo de “los diez años más calientes” o similar. Como si fuera algo para llevarse las manos a la cabeza. ¡Los diez años más calientes del registro están todos al final, #nosvamosamorir!
Por ejemplo, Seth Borenstein es un granado periodista de ciencia y verderío. Y dice [ABC News –>] [Wasington Post –>] :
Nueve de los diez años más calientes en el registro de la NOAA han ocurrido desde 2.000. La probabilidad de que eso ocurra aleatoriamente es como de una en 650 millones, de acuerdo con el estadístico de la Universidad de Carolina del Sur John Grego. Otros dos estadísticos lo han confirmado sus cálculos.
Ya está claro, y no hay ninguna duda, ¿no? ¡Joé, una probabilidad entre 650 millones! Nos vamos a morir todos. Salvo que prestes atención, y te des cuenta de un par de detalles. El primero, que si no fuera aleatorio no quiere decir que sí sea culpa de hombre. Los ciclos, tan característicos del clima, no son aleatorios -aunque podrían ser caóticos- y sí son naturales. Y segundo, que para que salga un cálculo así hay que partir de una idea estupefaciente. Concretamente, de la idea de que el clima juega a los dados cada año, y que cada tirada es independiente de la anterior. Por ejemplo, que si un año es muy caliente (o frío), el 31 de diciembre empieza un año nuevo sin calor (o frío) ninguno. La tierra se olvida de la temperatura que tiene el 31 de diciembre, y rompe la baraja cada año. Y todos somos subnormales.Y aunque es posible (pero muy raro) que Borenstein no sepa que hay otros tipos de procesos aleatorios, no es posible que los estadísticos que dice haber consultado no lo sepan. Pongamos un “camino aleatorio” [–>], donde el valor de temperatura de un año parte del valor del año anterior, y se le suma o resta una cantidad, aleatoriamente. Por ejemplo, cada año la temperatura varía -arriba o abajo- un poco, digamos 0,1ºC en promedio, y cada año en promedio tiene un valor de 0,1ºC más o menos que el anterior, aleatoriamente. Lo difícil es encontrar años muy calientes y muy fríos juntos; no años calientes seguidos, o años fríos seguidos.
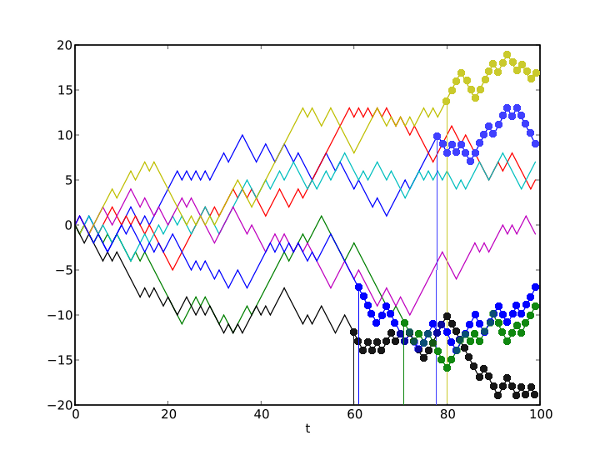
Una muestra muy lustrativa. En Wikipedia en inglés [–>], un tal Morn ha usado una fórmula para crear un gráfico con ocho ejemplos de “caminos aleatorios”. Y pone uno de los gráficos que le han salido:
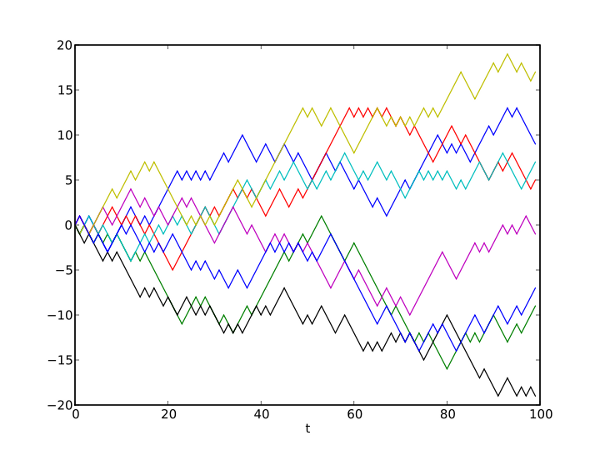Vale, pues de los ocho ejemplos, cinco le han salido con una probabilidad imposible – según Borenstein. En realidad, peor. En vez de ser nueve de los diez años más calientes entre los 15 últimos de una serie de 130 años, aquí vemos que salen todos los X años como los más calientes (o fríos), en una serie de cien años, donde X está entre 40 y 20 años seguidos como “los más calientes” de esa serie.
En la Wiki en español hay otro gráfico similar, hecho por otro autor, y de las ocho series son dos las que cumplen esas condiciones que para Borenstein y sus estadísticos son imposibles.
Pero pollo insiste [–>] con majaderías similares:
Texas A&M University climate scientist Andrew Dessler and other experts said the latest statistics should end claims by non-scientists that warming has stopped. It didn’t, as climate denial sites still touted claims that the world has not warmed in 18 years.
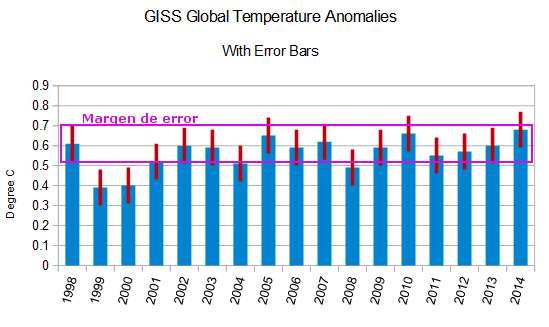
Pues no. Desde 1998 todos los años están en el margen de error -- o más abajo. Que por otra parte sólo es de una décima de grado (0,09º) arriba o abajo.
Fuente, y más completo y técnico, WUWT: